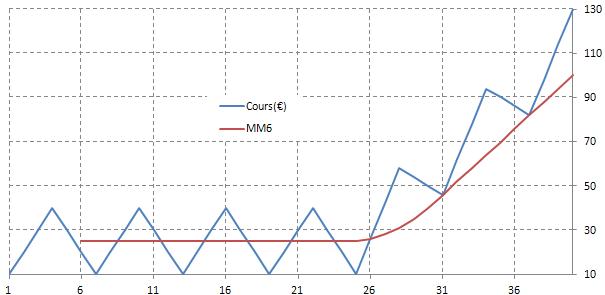
III-2 Dans le cas d’une hausse…
Que se passe-il si la moyenne progresse régulièrement avec un prix ayant ce même comportement cyclique ? Le prix évolue au-dessus la moyenne et nous avons cette « sensation » qu’il « rebondit » sur la moyenne mobile et repart à la hausse : elle agit comme un support à la baisse.
III-3 … ou d’une baisse.
A l’inverse si la moyenne mobile baisse régulièrement, le prix évolue sous la moyenne et semble repoussé vers le bas à chaque fois qu’il s’en approche : elle agit comme une résistance à la hausse. Entre ces deux phases, le comportement cyclique du prix s’est inversé !
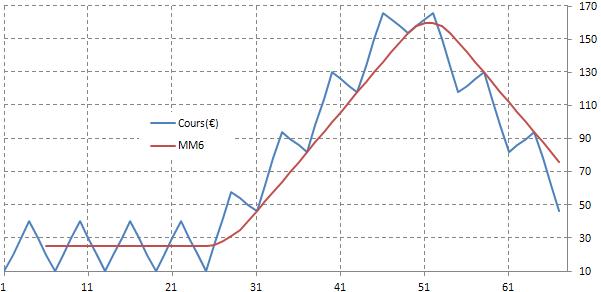
Cette propriété de la moyenne mobile a généré un certain nombre d’idées reçues, comme celle d’acheter aveuglément quand le prix s’approche d’une moyenne mobile haussière par exemple. Il ne faut pas oublier que ce type d’analyse repose sur 2 hypothèses empreintes de probabilité : la poursuite du comportement cyclique du prix, par conséquent celle de la régularité de la moyenne mobile. Dans ce cas on peut s’attendre légitimement que la moyenne mobile agit comme un « attracteur » lorsque le prix s’en éloigne de trop…
III-4 Cas des fortes et faibles tendances
Au cours de fortes hausses le comportement cyclique semble disparaître, en fait la phase de baisse du cycle est atténuée par la tendance haussière. Si la tendance haussière est très forte, la phase de baisse du cycle lorgne même vers le haut !
L’interprétation est analogue pour les tendances baissières mais avec des cycles inversés.
| Tendance haussière | Tendance baissière |
faible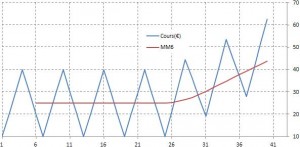 |
faible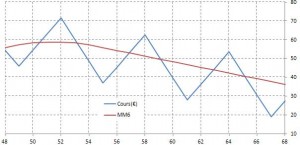 |
forte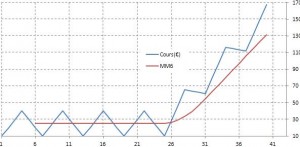 |
forte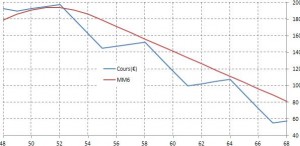 |
très forte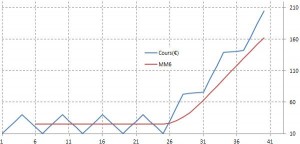 |
très forte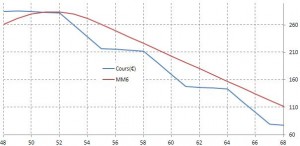 |